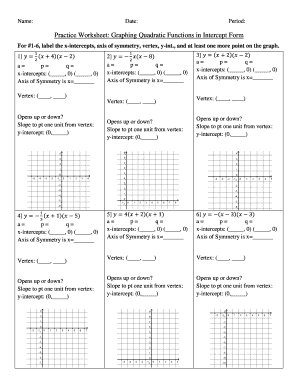
Get the free advanced math worksheet vertex form to standard form answer key
Show details
Worksheet: Standard form, line of symmetry and vertex for quadratic equations Name: Date: Mr. Chantal Practice writing quadratic equations in standard form and identifying a, b and c. Remember, standard
We are not affiliated with any brand or entity on this form
Get, Create, Make and Sign vertex form to standard form worksheet
Edit your standard to vertex form worksheet form online
Type text, complete fillable fields, insert images, highlight or blackout data for discretion, add comments, and more.
Add your legally-binding signature
Draw or type your signature, upload a signature image, or capture it with your digital camera.

Share your form instantly
Email, fax, or share your vertex to standard form worksheet with answers form via URL. You can also download, print, or export forms to your preferred cloud storage service.
How to edit converting from vertex form to standard form worksheet online
Follow the guidelines below to use a professional PDF editor:
1
Create an account. Begin by choosing Start Free Trial and, if you are a new user, establish a profile.
2
Simply add a document. Select Add New from your Dashboard and import a file into the system by uploading it from your device or importing it via the cloud, online, or internal mail. Then click Begin editing.
3
Edit quadratic equations in standard form worksheet. Rearrange and rotate pages, add and edit text, and use additional tools. To save changes and return to your Dashboard, click Done. The Documents tab allows you to merge, divide, lock, or unlock files.
4
Save your file. Choose it from the list of records. Then, shift the pointer to the right toolbar and select one of the several exporting methods: save it in multiple formats, download it as a PDF, email it, or save it to the cloud.
With pdfFiller, it's always easy to deal with documents. Try it right now
Uncompromising security for your PDF editing and eSignature needs
Your private information is safe with pdfFiller. We employ end-to-end encryption, secure cloud storage, and advanced access control to protect your documents and maintain regulatory compliance.
How to fill out standard form quadratic equation worksheet
How to fill out vertex to standard form:
01
Start by identifying the vertex of the quadratic equation. The vertex is represented as (h, k) in the equation y = a(x - h)^2 + k.
02
Determine the values of a, h, and k from the given quadratic equation.
03
Substitute the values of a, h, and k into the standard form equation y = a(x - h)^2 + k.
04
Simplify the equation and arrange it in standard form, which is typically written as y = ax^2 + bx + c, where a, b, and c are constants.
05
The resulting equation in standard form represents the original quadratic equation written with the vertex as the minimum or maximum point on the graph.
Who needs vertex to standard form:
01
Students studying algebraic concepts and quadratic equations in mathematics courses.
02
Engineers and scientists solving real-world problems that can be modeled using quadratic functions.
03
Anyone analyzing data sets or patterns that exhibit a quadratic relationship.
04
Individuals preparing for standardized tests or examinations that include quadratic equations.
05
Professionals working in fields such as economics, architecture, or physics, where understanding and interpreting quadratic equations are essential.
Fill
vertex to standard form worksheet
: Try Risk Free
Our user reviews speak for themselves
Read more or give pdfFiller a try to experience the benefits for yourself
For pdfFiller’s FAQs
Below is a list of the most common customer questions. If you can’t find an answer to your question, please don’t hesitate to reach out to us.
How do I edit standard form to vertex form worksheet with answers in Chrome?
Install the pdfFiller Chrome Extension to modify, fill out, and eSign your standard form to vertex form worksheet, which you can access right from a Google search page. Fillable documents without leaving Chrome on any internet-connected device.
How do I edit standard form of a quadratic equation worksheet on an iOS device?
You can. Using the pdfFiller iOS app, you can edit, distribute, and sign converting quadratic equations worksheet standard to vertex. Install it in seconds at the Apple Store. The app is free, but you must register to buy a subscription or start a free trial.
How can I fill out advanced math worksheet vertex form to standard form answers on an iOS device?
Make sure you get and install the pdfFiller iOS app. Next, open the app and log in or set up an account to use all of the solution's editing tools. If you want to open your converting standard form to vertex form worksheet, you can upload it from your device or cloud storage, or you can type the document's URL into the box on the right. After you fill in all of the required fields in the document and eSign it, if that is required, you can save or share it with other people.
What is advanced math worksheet vertex?
The advanced math worksheet vertex is a tool or document used to calculate and report certain mathematical values or variables, often in relation to financial or statistical analysis.
Who is required to file advanced math worksheet vertex?
Individuals or organizations that need to report specific mathematical computations or assessments related to their financial statements or tax filings are typically required to file the advanced math worksheet vertex.
How to fill out advanced math worksheet vertex?
To fill out the advanced math worksheet vertex, one must carefully input the required data and follow the provided instructions, ensuring all mathematical calculations are accurate and complete.
What is the purpose of advanced math worksheet vertex?
The purpose of the advanced math worksheet vertex is to simplify and standardize the process of reporting mathematical calculations for financial analysis and compliance with regulations.
What information must be reported on advanced math worksheet vertex?
Information that must be reported on the advanced math worksheet vertex typically includes mathematical calculations, financial data, supporting figures, and any relevant commentary required for clarity.
Fill out your advanced math worksheet vertex online with pdfFiller!
pdfFiller is an end-to-end solution for managing, creating, and editing documents and forms in the cloud. Save time and hassle by preparing your tax forms online.

Vertex Form Practice Worksheet is not the form you're looking for?Search for another form here.
Keywords relevant to vertex form to standard form worksheet answer key
Related to vertex form worksheet
If you believe that this page should be taken down, please follow our DMCA take down process
here
.